Reinforcement learning lab

This final lab is focused on helping you understand the reinforcement learning models we use in cognitive neuroscience. We want you to both realize their usefuleness but also their inherent limitations. Learning is complex--and reinforcement learning is able to capture many forms of learning. That said, there are many caveats, some of which we will discuss today. There is now an entire field dedicated to reinforcement learning but we're going to focus narrowly on just one specific idea: that you can estimate the value of an action by comparing your prediction against reality over and over.

Learning goals

After this lab you should have a better understanding of the following:

• How dopamine neurons encode a prediction error signal
• How the prediction error signal can be leveraged to learn the true value of an action by integrating over time
• Examples of when simple reinforcement algorithms are effective and when they fail

Demo

The first part of this tutorial is a live demonstration of reinforcement learning in action. You will take on the role of a squirrel. Your goal is to fatten yourself up to survive the Palo Alto winter. We all know how bad it can get, so collect a lot of apples! There will be three trees, each of which drops apples. Click on a tree to visit it--after a few seconds it will drop an apple (or a leaf, if you're unlucky). Some trees are better than others, so you'll have to search among all of the trees to find the best tree... good luck!

Head over to: our local forest to get started on the demo. Your TA will tell you which section to join.

Verbal model

Along with your class you should have had a discussion about a verbal model of learning in the apple hoarding task. Your model should have ended up being something like: "I keep an estimate of how many apples each tree drops in my mind. I pick a tree to go to and compare how many apples I get against what I expected. I adjust up or down accordingly". This is the verbal model that we're now going to translate into a computational one.

We've done this before so we're now going to dig into more of the details than we have in past computational models. The first thing to do here is to take the computational goal we've described (the verbal model) and turn it into a mathematical equation. This is important: our goal as cognitive neuroscientists is to connect the dots between behavior and the brain. Formalizing learning will allow us to make specific predictions, both about what should be represented by the brain but also about future behaviors. These predictions are the key to testing whether reinforcement learning is how a squirrel might solve this particular task.

The first part of our verbal model was: keep an estimate of how many apples each tree drops. For now we're going to model a world in which you make decisions about only one tree. What this means is that there's some variable that is going to keep track of our knowledge for a particular tree. We'll call this variable , for apples:

should probably start at our best guess about trees (before we get any information), which you could call your prior knowledge. We'll start at zero for simplicity, which sort of implies we're pessimistic. The second part of the verbal model says, "I pick a tree and compare how many apples I get against what I expected". Let's call the number of apples you get on each visit R, for reward. We'll call the difference between your knowledge and the reward the reward prediction error:

Notice that we indexed with a little ? That's because we're talking about a specific visit. Your knowledge about how many apples a tree drops is going to change over time so we need to be specific about when exactly we're talking about.

Reward prediction error

To help you get a sense for how prediction error is useful let's imagine a world with a single tree. On each step we're going to let you make a guess of how many apples will fall and then check your answer. We won't tell you how many apples actually fell, we're just going to tell you whether the prediction error was positive (more apples fell than you expected) or negative. The point of this demo is to reinforce the idea that you don't need absolute knowledge to do well at estimating something's value, as long as you can integrate information over time. This should remind you of a similar story we heard about LIP neurons and MT!

Guess: 0 Visit tree

Reward prediction error in the brain

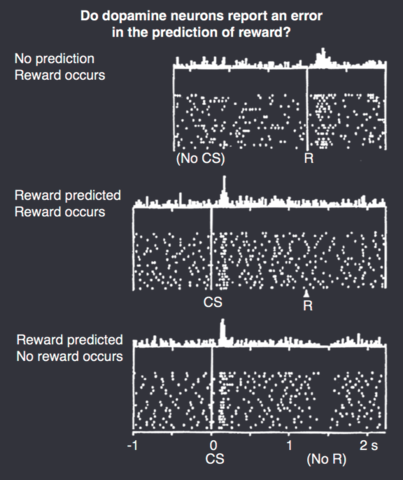
In lecture we learned about how neurons that produce dopamine encode the probability of rewards and their related uncertainty. Think back to your own experience: when you visited a tree you probably made a prediction about how many apples you would get--and then felt surprise or frustration when you got more or less than that amount. This is exactly the kind of information that we think dopamine neurons encode at different times. Take a look at the setup below. We have a squirrel who is going to imagine a tree (A, B, or C), you can click in the thought bubble to change which tree the squirrel is imagining. Tree A always drops an apple, tree B drops an apple half of the time, and tree C never drops an apple. On the right there's a recording of a dopamine neuron in the squirrel's ventral tegmental area. To see what happens when the squirrel actually visits a tree you can give the squirrel an apple, or not, by clicking on the apple or leaf at the bottom. In the neural trace you'll first see activity related to the squirrel predicting it's reward, then a moment later, the squirrel will receive the apple or leaf, and you'll see the neuron's response.

Before going on make sure you understand how this dopamine neuron circuit works:

• If the squirrel expects an apple and gets it, why doesn't the dopamine neuron fire for when the apple arrives?
• If the squirrel doesn't expect an apple and gets it, why then does the dopamine neuron fire?
• What happens in the intermediate conditions, when the squirrel believes that the tree only drops an occasional apple?

As a reminder about how dopamine neurons work, so that you can compare against what you get above, take a look at the plot below. It covers three of the conditions you can create above. Before you continue make sure you can re-create all three traces in the image as some combination of predictions and actual rewards for the squirrel.

Rescorla-Wagner

The last thing we need to think about is the learning rate. The intuition we want you to have for the learning rate is that it indexes how much you trust the reward prediction error. If there is a lot of variability in the world then you shouldn't trust it too much, you want a low learning rate to give yourself time to build up a good representation of the world. If the world is very stable and there isn't any noise then you can trust the reward prediction error precisely.

Adding the learning rate, the complete model that we've now built up looks as follows:

In English: to update our estimate of a tree's value (currently v, the next visit's predicted value will be v+1) we take our current prediction, , and add to it the reward prediction error, reduced by the learning rate which is shown as alpha.

Check out the graph below. It shows you the reward prediction error on each visit and the current estimate of the tree's value. We want you to get a sense for how the learning rate changes the evolution of over time--try tweaking the learning rate and then take a look at the examples we've put before.

Learning rate = 0.50

To help orient you to the graph go through these activities and make sure you understand each question before continuing:

• Try setting the learning rate to a very small value. What verbal model would this translate to? What would your decisions at each time point rely on?
• What if the learning rate is one? How then do your decisions change over time?
• Why does the RPE decrease, whereas the value increases and then stabilizes?
• What value does the learning rate need to be set to so that in the time span available the value stabilizes and the RPE is minimized. Can the RPE ever go to zero? Why/why not?

Exploit? Or explore?

So far your life as a squirrel has been easy. You were all alone in the forest visiting trees by yourself and nobody bothered you. But what would happen if other squirrels were visiting the trees along with you, is it still always optimal to head for the tree that drops the most apples? If everybody were to choose that same strategy, which we call exploiting, then someone would lose out. This is one of a few situations in which it can be advantageous to continue exploring the other options. Another situation in which this often comes up is when the value of a reward changes over time. Recall the Wisconsin card sort task--if the rules suddenly change and you stop being rewarded for the rule you are holding in mind it becomes advantageous to search for a new rule.

Competition

We're going to repeat the demonstration now, but with two changes. First, you're now going to be able to see the other students on the TA's screen. Second, everybody is now competing. The trees still only drop apples on some visits (some trees still drop apples more frequently), but now the stock of apples is limited. Even when a tree drops apples you might still get nothing. Should you persist at the tree you think is best? Or should you explore other options when this happens. We'll see who can come up with the best strategy! Connect to our local forest again and follow your TAs instructions. You'll have to wait for other students to catch up, so this is a good time to ask questions.

Tutorial complete!

Your TAs would be happy to discuss any aspect of the tutorial. As a reminder, you should now have a better understanding of the following:

• How dopamine neurons encode a prediction error signal
• How the prediction error signal can be leveraged to learn the true value of an action by integrating over time
• Examples of when simple reinforcement algorithms are effective and when they fail